improve R code efficiency

众所周知，当我们利用R语言处理大型数据集时，for循环语句的运算效率非常低。有许多种方法可以提升你的代码运算效率，但或许你更想了解运算效率能得到多大的提升。本文将介绍几种适用于大数据领域的方法，包括简单的逻辑调整设计、并行处理和Rcpp的运用，利用这些方法你可以轻松地处理1亿行以上的数据集。
让我们尝试提升往数据框中添加一个新变量过程(该过程中包含循环和判断语句)的运算效率：

实验环境：

1
2
3
R version 3.3.1 (2016-06-21)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 7 x64 (build 7601) Service Pack 1

实验数据集　

1
2
3
4
5
6

col1 <- runif (12^5, 0, 2)
col2 <- rnorm (12^5, 0, 2)
col3 <- rpois (12^5, 3)
col4 <- rchisq (12^5, 2)
df <- data.frame (col1, col2, col3, col4)

0.原始方法

逐行判断该数据框(df)的总和是否大于4，如果该条件满足，则对应的新变量数值为’greaterthan’，否则赋值为’lesserthan’。

1
2
3
4
5
6
7
8
9
10
# Original R code: Before vectorization and pre-allocation
system.time({
  for (i in 1:nrow(df)) { # for every row
    if ((df[i, 'col1'] + df[i, 'col2'] + df[i, 'col3'] + df[i, 'col4']) > 4) { # check if > 4
      df[i, 5] <- "greater_than_4" # assign 5th column
    } else {
      df[i, 5] <- "lesser_than_4" # assign 5th column
    }
  }
})

用户 系统 流逝
810.11 146.06 965.80

1.向量化处理和预设数据库结构

循环运算前，记得预先设置好数据结构和输出变量的长度和类型，千万别在循环过程中渐进性地增加数据长度。接下来，我们将探究向量化处理是如何提高处理数据的运算速度。

1
2
3
4
5
6
7
8
9
10
11
# after vectorization and pre-allocation
output <- character (nrow(df)) # initialize output vector
system.time({
  for (i in 1:nrow(df)) {
    if ((df[i, 'col1'] + df[i, 'col2'] + df[i, 'col3'] + df[i, 'col4']) > 4) {
      output[i] <- "greater_than_4"
    } else {
      output[i] <- "lesser_than_4"
    }
  }
})

用户 系统 流逝
28.27 0.05 28.98

2.将条件语句的判断条件移至循环外

将条件判断语句移至循环外可以提升代码的运算速度，接下来本文将利用包含100,000行数据至1,000,000行数据的数据集进行测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
# after vectorization and pre-allocation, taking the condition checking outside the loop.
output <- character (nrow(df))
condition <- (df$col1 + df$col2 + df$col3 + df$col4) > 4  # condition check outside the loop
system.time({
  for (i in 1:nrow(df)) {
    if (condition[i]) {
      output[i] <- "greater_than_4"
    } else {
      output[i] <- "lesser_than_4"
    }
  }
 
})

用户 系统 流逝
0.37 0.01 0.39

3.只在条件语句为真时执行循环过程

另一种优化方法是预先将输出变量赋值为条件语句不满足时的取值，然后只在条件语句为真时执行循环过程。此时，运算速度的提升程度取决于条件状态中真值的比例。
本部分的测试将和case(2)部分进行比较，和预想的结果一致，该方法确实提升了运算效率。

1
2
3
4
5
6
7
8
9
10
output <- c(rep("lesser_than_4", nrow(df)))
condition <- (df$col1 + df$col2 + df$col3 + df$col4) > 4
system.time({
    for (i in (1:nrow(df))[condition]) {  # run loop only for true conditions
        if (condition[i]) {
            output[i] <- "greater_than_4"
        } 
    }
   
})

4.尽可能地使用 ifelse()语句

利用ifelse()语句可以使你的代码更加简便。ifelse()的句法格式类似于if()函数，但其运算速度却有了巨大的提升。即使是在没有预设数据结构且没有简化条件语句的情况下，其运算效率仍高于上述的两种方法。

1
2
3
system.time({
  output <- ifelse ( rowSums(df) > 4, "greater_than_4", "lesser_than_4")
})

用户 系统 流逝 0.08 0.00 0.07

5.使用 which()语句

利用which()语句来筛选数据集，我们可以达到Rcpp三分之一的运算速率。

1
2
3
4
5
6
system.time({
  want = which(rowSums(df) > 4)
  output = rep("less than 4", times = nrow(df))
  output[want] = "greater than 4"
}) 
# nrow = 3 Million rows (approx)

用户 系统 流逝 0.02 0.00 0.01

6.利用apply族函数来替代for循环语句

本部分将利用apply()函数来计算上文所提到的案例，并将其与向量化的循环语句进行对比。该方法的运算效率优于原始方法，但劣于ifelse()和将条件语句置于循环外端的方法。该方法非常有用，但是当你面对复杂的情形时，你需要灵活运用该函数。

1
2
3
4
5
6
7
8
9
10
11
# apply family
system.time({
  myfunc <- function(x) {
    if ((x['col1'] + x['col2'] + x['col3'] + x['col4']) > 4) {
      "greater_than_4"
    } else {
      "lesser_than_4"
    }
  }
  output <- apply(df[, c(1:4)], 1, FUN=myfunc)  # apply 'myfunc' on every row
})

用户 系统 流逝 1.4 0.0 1.4

7.利用compiler包中的字节码编译函数cmpfun()

这可能不是说明字节码编译有效性的最好例子，但是对于更复杂的函数而言，字节码编译将会表现地十分优异，因此我们应当了解下该函数。

1
2
3
4
5
6
# byte code compilation
library(compiler)
myFuncCmp <- cmpfun(myfunc)
system.time({
  output <- apply(df[, c (1:4)], 1, FUN=myFuncCmp)
})

用户 系统 流逝 1.10 0.00 1.11

8.利用Rcpp

截至目前，我们已经测试了好几种提升运算效率的方法，其中最佳的方法是利用ifelse()函数。如果我们将数据量增大十倍，运算效率将会变成啥样的呢？接下来我们将利用Rcpp来实现该运算过程，并将其与ifelse()进行比较。

1
2
3
library(Rcpp)
sourceCpp("MyFunc.cpp")
system.time (output <- myFunc(df))

see Rcpp function below

下面是利用C++语言编写的函数代码，将其保存为“MyFunc.cpp”并利用sourceCpp进行调用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// Source for MyFunc.cpp
#include 
using namespace Rcpp;
// [[Rcpp::export]]
CharacterVector myFunc(DataFrame x) {
  NumericVector col1 = as(x["col1"]);
  NumericVector col2 = as(x["col2"]);
  NumericVector col3 = as(x["col3"]);
  NumericVector col4 = as(x["col4"]);
  int n = col1.size();
  CharacterVector out(n);
  for (int i=0; i 4){
      out[i] = "greater_than_4";
    } else {
      out[i] = "lesser_than_4";
    }
  }
  return out;
}

9.利用并行运算

并行运算的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# parallel processing
library(foreach)
library(doSNOW)
cl <- makeCluster(4, type="SOCK") # for 4 cores machine
registerDoSNOW (cl)
condition <- (df$col1 + df$col2 + df$col3 + df$col4) > 4
# parallelization with vectorization
system.time({
  output <- foreach(i = 1:nrow(df), .combine=c) %dopar% {
    if (condition[i]) {
      return("greater_than_4")
    } else {
      return("lesser_than_4")
    }
  }
})

用户 系统 流逝 186.72 7.13 202.87

10.尽早地移除变量并回收内存

在进行冗长的循环计算前，尽早地将不需要的变量移除掉，使用rm()函数。在每次循环迭代运算结束时利用gc()函数恢复内存也可以提升运算速率。

11.利用内存较小的数据结构

data.table()是一个很好的例子，因为它可以减少数据的内存，这有助于加快运算速率。

1
2
3
4
5
6
7
8
9
10
11
12

library(data.table)
dt <- data.table(df)  # create the data.table
system.time({
  for (i in 1:nrow (dt)) {
    if ((dt[i, col1] + dt[i, col2] + dt[i, col3] + dt[i, col4]) > 4) {
      dt[i, col5:="greater_than_4"]  # assign the output as 5th column
    } else {
      dt[i, col5:="lesser_than_4"]  # assign the output as 5th column
    }
  }
})

用户 系统 流逝

629.89 0.31 640.91

总结

方法：速度， nrow(df)/time_taken = n 行每秒

原始方法：1X, 856.2255行每秒(正则化为1)
向量化方法：738X, 631578行每秒
只考虑真值情况：1002X，857142.9行每秒
ifelse：1752X，1500000行每秒
which：8806X，7540364行每秒
Rcpp：13476X，11538462行每秒

参考链接：(http://datascienceplus.com/strategies-to-speedup-r-code/)

R语言

Feature Selection

1.特征选择的概述

1.1 特征工程的简介

相信每一个数据人都深刻地体会过这样一句话：“特征工程做不好，调参调到老”。业界更有这样的说法：“数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已”。由此可见，特征工程在机器学习中占有相当重要的地位。到底什么是特征工程，我认为并没有确切的定义，个人是这样理解的：特征工程是利用业务领域和数据科学领域的相关知识，创建使机器学习算法达到最优的特征的过程。特征工程主要包括特征抽取和特征选择两部分。特征抽取主要是依据相关领域知识提取特征，更多的依靠业务知识。下文将重点介绍特征选择。

1.2 特征选择的简介

(1) 什么是特征选择

特征选择 ( Feature Selection )也称特征子集选择( Feature Subset Selection , FSS ) ，或属性选择( Attribute Selection ) ，是指从全部特征中选取一个特征子集，使构造出来的模型更好。

(2) 为什么要做特征选择

在机器学习的实际应用中，特征数量往往较多，其中可能存在不相关的特征，特征之间也可能存在相互依赖，容易导致如下的后果：

  • 特征个数越多，分析特征、训练模型所需的时间就越长。
  • 特征个数越多，容易引起“维度灾难”，模型也会越复杂，其推广能力会下降。
  • 特征选择能剔除不相关(irrelevant)或冗余(redundant )的特征，从而达到减少特征个数，提高模型精确度，减少运行时间的目的。
  • 选取出真正相关的特征简化了模型，使研究人员易于理解数据产生的过程。

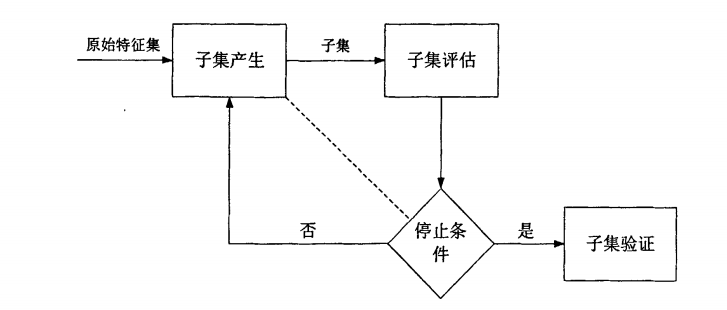
1.3 特征选择的过程

Dash和Liu提出了一个特征选择的基本框架，认为一个典型的特征选择
算法由图所示的4个基本步骤组成

特征选择的过程

(1)子集产生：按照一定的搜索策略产生候选特征子集。

(2)子集评估：通过某个评价函数评估特征子集的优劣。

(3)停止条件：决定特征选择算法什么时候停止。

(4)子集验证：用于验证最终所选的特征子集的有效性。

这四个步骤组成了一个完整的特征选择过程。

  • 子集产生是一个搜索过程， 用来产生待评价的特征子集。搜索过程的起始点可以是：不含任何特征的空集；含所有特征的全部特征集；随机的一个特征子集。前面两种情况，特征是迭代地添加或移除。
  • 子集评估过程用于评价特征子集的优劣，即根据某个评价函数对子集进行评价，每进行一次特征子集的优劣评价，将新的评价值和之前保存的最优评价值进行比较，如果新的子集的评价值更优，则用它来取代之前的最优评价值。
  • 子集评估之后要进行停止条件的判断，如果没有停止条件，搜索过程将无法停止。如图所示，子集产生和子集评估都可能影响到停止条件的选择，基于子集产生的停止条件有：a．达到预先指定的特征数目。b．达到预先给定的迭代次数。基于子集评估的停止条件有：a．增加或减少特征不能使特征子集的评价值有所提高。b．使评价函数取最优解的特征子集已经找到。
  • 子集有效性验证是特征选择的最后一个步骤，在实际应用中是必不可少的，有效性验证通常用经过特征选择算法处理后的数据集进行训练和预测，将训练和预测的结果和在原始数据集上的结果进行比较，比较的内容包括预测的准确性、模型的复杂程度等。

2.特征选择常用的方法

  • 按照特征子集的形成方式可以分为三种：完全搜索(Complete)、启发式搜索（heuristic）和随机搜索。
  • 按照特征评价标准来分，根据评价函数与模型的关系，可以分为筛选式、封装式和嵌入式三种。

2.1 基于特征子集的形成方式的特征选择方法

基于特征子集的形成方式的特征选择方法主要有完全搜索(Complete)、启发式搜索(Heuristic)和随机搜索。

特征选择本质上是一个组合优化问题，求解组合优化问题最直接的方法就是搜索，理论上可以通过穷举法来搜索所有可能的特征组合，选择使得评价标准最优的特征子集作为最后的输出。如果我们有N个特征变量，则特征变量的状态集合中的元素个数就是$2^N$，通过穷举的方式进行求解的时间复杂度是指数级的 (O(2^{N} ))。

为了减少运算量，目前特征子集的搜索策略大都采用贪心算法（greedy algorithm），其核心思想是在每一步选择中，都采纳当前条件下最好的选择，从而获得组合优化问题的近似最优解。根据其实现的细节，又可将贪心算法分为三种：前向搜索 (forward search)，后向搜索(backward search)和双向搜索 (bidirectional search)。

假定我们有一个特征集合${a_{1},a_{2},...,a_{d}}$,前向搜索的思想是:

  • 第一步我们可以将每一个特征看成一个候选子集，例如依据给定的评价标准，特征${a_{1}}$的效果最优，则子集为${a_{1}}$,于是将${a_{1}}$做为第一轮的选定集；
  • 第二步，则是往已有的子集中加入下一个效果最优的特征变量，例如对于子集${a_{1},a_{i}}$，当 i=2 时效果最优，则新的子集确定为${a_{1},a_{2}}$。如此重复进行搜索，直到新一轮获得的子集效果不如前一轮，则搜索停止。

后向搜索的做法，是以包含全部特征的集合开始，逐步剔除特征，直到找到效果最优的子集。双向搜索则把前向搜索和后向搜索结合起来，不断在选定的子集中加入新特征，并同时剔除旧特征。

因为采取的是贪心算法，它们仅考虑使本轮的子集最优，例如在第三轮假定选择$a_{5}$优于$a_{6}$,于是该轮的最优子集为${a_{1},a_{2},a_{5}}$，然后再第四轮中却可能是${a_{1},a_{2},a_{6},a_{8}}$比所有的${a_{1},a_{2},a_{5},a_{i}}$都更优。但是，若不进行穷举搜索，则这样的问题无法避免。

这三类算法在R语言的stats包和MASS包中的线性回归建模中都实现了。

2.2 基于评价准测的特征选择方法

按照特征评价标准来分，根据评价函数与模型的关系，可以分为筛选式、封装式和嵌入式三种。

2.2.1 过滤式(Filter)

通常把先进行特征选择，再进行建模的方法称为过滤式（filter），它主要侧重于单个特征跟目标变量的相关性，此时特征选择的标准和模型优化标准并不一定相同，和下一步将要使用的机器学习算法没有必然联系。

Dash和Liu把过滤式特征选择的评价标准分为四种，即关联度度量、距离度量、信息度量、以及一致性度量。

  • 关联性度量：
    主要考察特征和类别的关联度以及特征间的关联度，即通常所说的相关性和冗余性。关联性度量有线性关联(如Pearson相关系数)和非线性关联(如基于信息熵的互信息、对称的不确定性等)
  • 距离度量：运用距离度量进行特征选择是基于这样的假设：好的特征子集应该使得属于同一类的样本距离尽可能小，属于不同类的样本之间的距离尽可能远。常用的距离度量（相似性度量）包括欧氏距离、标准化欧氏距离、马氏距离以及基于概率距离度量的KL散度等。
  • 信息度量：信息度量是把信息论中基于熵的评估标准应用得到特征选择中，如信息增益(Information Gain)、信息增益率(Information Gain Ratio)、基尼指数(Gini Index)、WOE(Weight of Evidence)以及IV(Informationvalue)等。
  • 一致性度量：试图找到与全集相同分类能力的最小特征子集。不一致性定义为如果两个样本在选定的特征子集上取值相同，却属于不同的类。

下面简单地介绍常见的评价函数：

(1) Pearson相关系数

Pearson相关系数的数学公式为：$r=\frac{cov(X,Y)}{\sqrt{var(X)var(Y)}}$

Pearson相关系数是最常用的判断特征和响应变量（response variable）之间的线性关系的标准。结果的取值区间为[-1，1]，-1表示完全的负相关+1表示完全的正相关，0表示没有线性相关。
Pearson 相关系数的优点在于其计算简单，结果易于理解且易于比较；而其缺点在于不能反映变量之间的非线性关系,如果关系是非线性的，即便两个变量具有一一对应的关系，Pearson相关性也可能会接近0。

Python中，Scipy的 pearsonr 方法能够同时计算相关系数和p-value

1
2
3
4
5
import numpy as np
from scipy.stats import pearsonr
x = np.random.normal(0, 1, 100)
print pearsonr(x, x**2)[0]
-0.2072

在R中，用cor函数求相关系数

1
2
3
x <- rnorm(100)
cor(x,x^2)
-0.132433

(2)信息增益(Information Gain)

假设存在离散变量Y，Y中的取值包括{y1,y2,…,ym} ，yi出现的概率为Pi。则Y的信息熵定义为：
$$H(Y)=-\sum_{i=1}^{m}P_{i}logP_{i}$$

信息熵有如下特性：若集合Y的元素分布越“纯”，则其信息熵越小；若Y分布越“混乱”，则其信息熵越大。在极端的情况下：若Y只能取一个值，即P1=1，则H(Y)取最小值0；反之若各种取值出现的概率都相等，即都是1/m，则H(Y)取最大值$log_{2}m$。

在附加条件另一个变量X，而且知道$X=x_{i}$后，Y的条件信息熵(Conditional Entropy)表示为：
$$H(Y|X)=\sum_{i=1}^{m}P_{x=x_{i}}H(Y|X=x_{i})$$
在加入条件X前后的Y的信息增益定义为:
$$IG(Y|X)=H(Y)-H(Y|X)$$
假设存在特征子集A和特征子集B，分类变量为C，若IG( C|A ) > IG( C|B ) ，则认为选用特征子集A的分类结果比B好，因此倾向于选用特征子集A。

(3)最大信息系数(Mutual information and maximal information coefficient,MIC)

Pearson相关系数不能反映变量之间的非线性关系；信息增益直接用于特征选择时通常变量需要先离散化，而且信息增益的结果对离散化的方式很敏感。但是最大信息系数克服了这两个问题。它首先寻找一种最优的离散化方式，然后把互信息取值转换成一种度量方式，取值区间在[0，1]。

MIC的性质：

  • 对于所有无噪声并且非常数的函数关系，MIC的值都为1
  • 对于两个有确定的函数关系的随机变量，不论这个函数关系是什么样的，MIC的值都是1
  • 对于两个统计独立的随机变量MIC的值接近于0

Python中，minepy 提供了MIC功能。

反过头来看$y=x^2$这个例子，MIC算出来的互信息值为1(最大的取值)。

1
2
3
4
5
6
from minepy import MINE
m = MINE()
x = np.random.normal(0,1,100)
m.compute_score(x, x**2)
print m.mic()
1

R中minerva包的mine函数可直计算出mic的值。

1
2
3
4
library(minerva)
x <- rnorm(100)
mine(x,y=x^2)$MIC
[1] 1

可以看出，虽然x与$y=x^2$是函数关系，Pearson相关系数却很相小，但是通过MIC为1可以发现二者之间强烈的非线性关系。

(4)距离相关系数 (Distance correlation)

距离相关系数是针对 Pearson 相关系数只能表征线性关系的缺点而提出的。其思想是分别构建特征变量和响应变量的欧氏距离矩阵，并由此计算特征变量和响应变量的距离相关系数。详细的定义和计算过程可参考维基百科。

距离相关系数能够同时捕捉变量之间的线性和非线性相关。当距离相关系数为 0，则可断言两个变量相互独立（Pearson 相关系数为 0 不代表变量相互独立）。其缺点是与 Pearson 相关系数相比，其所需的运算量较大，而且取值范围为 [0, 1]，无法表征变量之间关联是正相关还是负相关。

R的 energy 包里提供了距离相关系数的实现

1
2
3
x <- rnorm(100)
dcor(x, x**2)
0.5880842

(5)WOE和IV

WOE是一种基于目标变量的自变量编码方式，信用评分卡模型中最常用这种编码方式。例如将模型目标标量为1记为违约用户，对于目标变量为0记为正常用户；则WOE(weight of Evidence)其实就是自变量取某个值的时候对违约比例的一种影响。

WOE的公式：$$woe_{i}=ln(\frac{p_{y=1}}{p_{y=0}})$$

IV的公式：$$IV_{i}=(p_{y=1}-p_{y=0})\times woe_{i}$$

那么， $$IV=\sum_{i=1}^{k}IV_{i}$$

例如下表：

变量(age) bad(y=1人数) good(y=0的人数) woe IV
0-18 10 50 log((10/40)/(50/100)) {(10/40)-(50/100)}log((10/40)/(50/100))
18-30 10 20 log((10/40)/(20/100)) {(10/40)-(20/100)}log((10/40)/(20/100))
30-50 20 30 log((20/40)/(30/100)) {(20/40)-(30/100)}log((20/40)/(30/100))
sum 40 100

表中以age年龄为某个自变量，由于年龄是连续型自变量，需要对其进行离散化处理，假设离散化分为3组，bad和good表示在这三组中违约用户和正常用户的数量分布，可以计算出每一组的WOE值和IV值，通过后面的公式可以看出，woe反映的是在自变量每个分组下违约用户对正常用户占比和总体中违约用户对正常用户占比之间的差异；从而可以直观的认为woe蕴含了自变量取值对于目标变量（违约概率）的影响。

该变量age的IV值为：
$$IV=\sum_{i=1}^{3}IV_{i}$$

  • 从公式来看的话，其实IV衡量的是某一个变量的信息量，相当于是自变量woe值的一个加权求和，其值的大小决定了自变量对于目标变量的影响程度
  • 从另一个角度来看的话，IV公式与信息熵的公式极其相似。
  • 变量的IV值表示着该变量对因变量的区分度，IV值越大，该变量的越有价值，从而可以用IV值来进行特征选择。

2.2.2 包裹式(Wrapper)

而把特征选择和模型优化的标准统一起来的方法则有包裹式（wrapper）和嵌入式（embedding）。包裹式的方法以模型的优化标准作为特征选择的标准，但仍然把特征选择和模型训练分为两个步骤。与过滤式特征选择不考虑后续学习器不同，包裹式特征选择直接把最终将要使用的学习器的性能作为特征子集的评价标准，比如准确率、召回率、AUC值、AIC 准则和 BIC 准则等评价标准。

  • 赤池信息准则（Akaike information criterion, AIC）
    $$AIC=2k-2ln(L)$$
  • 贝叶斯信息准则（Bayesian Information Criterions, BIC）
    $$BIC=ln(n)*k-2ln(L)$$

其中k为参数数目，$L$是似然函数（likelihood function）,n是数据中观测值的数量。

AIC 和 BIC 的表达式中均包含了模型复杂度惩罚项和最大似然函数项。不同的地方在于，在 BIC 的表达式中，惩罚项的权重随观测值的增加而增加。因此当观测值数量较大时，只有显著关联的特征变量才会被保留，从而降低模型的复杂性。

在建模时，我们可以通过最小化 AIC 或 BIC 来选择模型的最优参数。由表达式可以看出，AIC 和 BIC 倾向于复杂度低（越小越好）和符合先验假设（越大越好）的模型。在简单线性回归中，似然函数是依据残差服从正态分布的先验假设构建的，即如果特征变量的加入能够使残差更接近正态分布，则认为这个特征能够显著改善线性回归模型。

2.2.3 嵌入式(Embedded)

嵌入式则是把特征选择和模型训练融为一体，两者在同一个优化的过程中完成，不再分为两个步骤，即在学习器训练过程中自动的进行了特征选择。最典型的有L1正则化以及决策树算法，如ID3、C4.5和CART算法等，决策树算法在树增长过程的每个递归步都必须选择一个特征，将样本集划分成较小的子集，选择特征的依据通常是划分后子节点的纯度，划分后子节点越纯，则说明划分效果越好，可见决策树生成的过程也就是特征选择的过程。

(1) L1正则化

在优化理论中，正则化（regularization）是一类通过对解施加先验约束把不适定问题（ill-posed problem）转化为适定问题的常用技巧。例如，在线性回归模型中，当用最小二乘法估计线性回归的系数时，如果自变量存在共线性，系数的估计值将具有较大的方差，因而会影响后续参数的统计检验。如果在最小二乘法的参数估计表达式中添加L1正则项，则称为Lasso线性回归模型：

$$\widehat{\beta }=arg min_{\beta}[(Y-\beta X)^{T}(Y-\beta X)+\lambda|\beta|]$$

L1正则化将系数w的L1范数作为惩罚项加到损失函数上，由于正则项非零，这就迫使那些弱的特征所对应的系数变成0。因此L1正则化往往会使学到的模型很稀疏（系数w经常为0），这个特性使得L1正则化成为一种很好的特征选择方法。线性回归有Lasso回归，分类模型有L1逻辑回归。

(2) 基于树的模型

基于树的模型，如随机森林、GBDT、XGBOOST等都可以输出变量的重要度，从而达到特征选择的作用。

  • 平均不纯度减少 (mean decrease impurity)

决策树中的每一个节点都是关于某个特征的条件，为的是将数据集按照不同的响应变量一分为二。利用不纯度可以确定节点（最优条件），对于分类问题，通常采用基尼不纯度或者信息增益 ，对于回归问题，通常采用的是方差或者最小二乘拟合。当训练决策树的时候，可以计算出每个特征减少了多少树的不纯度。对于一个决策树森林来说，可以算出每个特征平均减少了多少不纯度，并把它平均减少的不纯度作为特征选择的值。

  • 平均精确率减少 (Mean decrease accuracy)

另一种常用的特征选择方法就是直接度量每个特征对模型精确率的影响。主要思路是打乱每个特征的特征值顺序，并且度量顺序变动对模型的精确率的影响。很明显，对于不重要的变量来说，打乱顺序对模型的精确率影响不会太大，但是对于重要的变量来说，打乱顺序就会降低模型的精确率。

(3)递归特征消除 (Recursive feature elimination ,RFE)

递归特征消除的主要思想是反复的构建模型（如SVM或者回归模型）然后选出最好的（或者最差的）的特征（可以根据系数来选），把选出来的特征放到一边，然后在剩余的特征上重复这个过程，直到所有特征都遍历了。这个过程中特征被消除的次序就是特征的排序。因此，这是一种寻找最优特征子集的贪心算法。

RFE的稳定性很大程度上取决于在迭代的时候底层用哪种模型。例如，假如RFE采用的普通的回归，没有经过正则化的回归是不稳定的，那么RFE就是不稳定的；假如采用的是Ridge，而用Ridge正则化的回归是稳定的，那么RFE就是稳定的。

Python 的 scikit-learn 模块中提供了一种循环特征剔除 (recursive feature elimination, RFE) 的实现，遵循的也是后向搜索的思路。

3 代码演练

(1) 基于前向搜索、后向搜索和双向搜索的回归模型在R中的实现：

这三类算法在R语言的stats包和MASS包中的线性回归建模中都实现了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
library(MASS)
initial <- glm(Class ~ tau + VEGF + E4 + IL_3, data = training, family = binomial)
stepAIC(initial, direction = "both")
Start: AIC=189.46
Class ~ tau + VEGF + E4 + IL_3

Df Deviance AIC
- IL_3 1 179.69 187.69
- E4 1 179.72 187.72
<none> 179.46 189.46
- VEGF 1 242.77 250.77
- tau 1 288.61 296.61

Step: AIC=187.69
Class ~ tau + VEGF + E4

Df Deviance AIC
- E4 1 179.84 185.84
<none> 179.69 187.69
+ IL_3 1 179.46 189.46
- VEGF 1 248.30 254.30
- tau 1 290.05 296.05

Step: AIC=185.84
Class ~ tau + VEGF

Df Deviance AIC
<none> 179.84 185.84
+ E4 1 179.69 187.69
+ IL_3 1 179.72 187.72
- VEGF 1 255.07 259.07
- tau 1 300.69 304.69

Call: glm(formula = Class ~ tau + VEGF, family = binomial, data = training)

Coefficients:
(Intercept) tau VEGF
9.8075 -4.2779 0.9761

Degrees of Freedom: 266 Total (i.e. Null); 264 Residual
Null Deviance: 313.3
Residual Deviance: 179.8 AIC: 185.8

基于AIC准则，通过双向搜索我们得到了最优的分类模型。

(2) 基于IV的特征变量选择在R中的实现：

在R中，smbinning包可以做变量的分箱、计算woe以及IV。用其自带数据集举例如下：

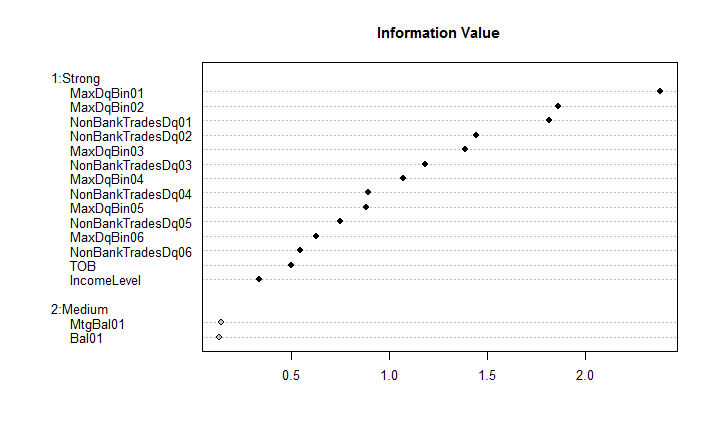
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# Package loading and data exploration
library(smbinning) # Load package and its data
data(chileancredit) # Load smbinning sample dataset (Chilean Credit)
str(chileancredit) # Quick description of the data

'data.frame':	7702 obs. of  19 variables:
 $ CustomerId       : chr  "0000000185" "0000000238" "0000000346" "0000000460" ...
 $ TOB              : int  44 79 102 NA 109 183 172 76 136 171 ...
 $ IncomeLevel      : Factor w/ 6 levels "0","1","2","3",..: 2 2 2 2 NA NA 1 2 1 1 ...
 $ Bal01            : num  605 1006 299 645 218 ...
 $ MaxDqBin01       : Factor w/ 7 levels "0","1","2","3",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ MaxDqBin02       : Factor w/ 8 levels "0","1","2","3",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ MaxDqBin03       : Factor w/ 8 levels "0","1","2","3",..: 1 1 1 1 1 1 1 2 1 1 ...
 $ MaxDqBin04       : Factor w/ 8 levels "0","1","2","3",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ MaxDqBin05       : Factor w/ 8 levels "0","1","2","3",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ MaxDqBin06       : Factor w/ 8 levels "0","1","2","3",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ MtgBal01         : num  0 0 0 0 0 0 0 0 0 0 ...
 $ NonBankTradesDq01: int  0 0 0 0 0 0 0 0 0 0 ...
 $ NonBankTradesDq02: int  0 0 0 0 0 0 0 0 0 0 ...
 $ NonBankTradesDq03: int  0 0 0 0 0 0 0 0 0 0 ...
 $ NonBankTradesDq04: int  0 0 0 0 0 0 0 1 0 0 ...
 $ NonBankTradesDq05: int  0 0 0 0 0 0 0 1 0 0 ...
 $ NonBankTradesDq06: int  0 0 0 0 0 0 0 1 0 0 ...
 $ FlagGB           : int  1 1 1 1 1 1 1 1 1 1 ...
 $ FlagSample       : int  1 1 1 1 1 1 1 1 1 1 ...
 
table(chileancredit$FlagGB) # Tabulate target variable

 0    1 
 636 5654
 
# Training and testing samples (Just some basic formality for Modeling)
chileancredit.train=subset(chileancredit,FlagSample==1)
chileancredit.test=subset(chileancredit,FlagSample==0)
# Package application
result=smbinning(df=chileancredit.train,y="FlagGB",x="TOB",p=0.05) # Run and save result
result$ivtable # Tabulation and Information Value

Cutpoint CntRec CntGood CntBad CntCumRec CntCumGood CntCumBad PctRec GoodRate
1    <= 17   1138     909    229      1138        909       229 0.2405   0.7988
2    <= 30    621     530     91      1759       1439       320 0.1312   0.8535
3    <= 63   1064     985     79      2823       2424       399 0.2249   0.9258
4     > 63   1427    1377     50      4250       3801       449 0.3016   0.9650
5  Missing    482     435     47      4732       4236       496 0.1019   0.9025
6    Total   4732    4236    496        NA         NA        NA 1.0000   0.8952
  BadRate    Odds LnOdds     WoE     IV
1  0.2012  3.9694 1.3786 -0.7662 0.1893
2  0.1465  5.8242 1.7620 -0.3828 0.0223
3  0.0742 12.4684 2.5232  0.3784 0.0277
4  0.0350 27.5400 3.3156  1.1708 0.2626
5  0.0975  9.2553 2.2252  0.0804 0.0006
6  0.1048  8.5403 2.1448  0.0000 0.5025

# Summary IV application
sumivt=smbinning.sumiv(chileancredit.train,y="FlagGB")
sumivt # Display table with IV by characteristic

  Char     IV                  Process
5         MaxDqBin01 2.3771        Factor binning OK
6         MaxDqBin02 1.8599        Factor binning OK
12 NonBankTradesDq01 1.8129       Numeric binning OK
13 NonBankTradesDq02 1.4417       Numeric binning OK
7         MaxDqBin03 1.3856        Factor binning OK
14 NonBankTradesDq03 1.1819       Numeric binning OK
8         MaxDqBin04 1.0729        Factor binning OK
15 NonBankTradesDq04 0.8948       Numeric binning OK
9         MaxDqBin05 0.8844        Factor binning OK
16 NonBankTradesDq05 0.7511       Numeric binning OK
10        MaxDqBin06 0.6302        Factor binning OK
17 NonBankTradesDq06 0.5501       Numeric binning OK
2                TOB 0.5025       Numeric binning OK
3        IncomeLevel 0.3380        Factor binning OK
11          MtgBal01 0.1452       Numeric binning OK
4              Bal01 0.1379       Numeric binning OK
1         CustomerId     NA   Not numeric nor factor
18        FlagSample     NA Uniques values of x < 10

# Plotting smbinning.sumiv
smbinning.sumiv.plot(sumivt,cex=0.8) # Plot IV summary table

IV

通过IV的大小进行特征排序，从而达到特征选择的目的。

(3) 基于L1正则化的特征变选择在R中的实现：

R语言中glmnet包可以实现L1正则化、L2正则化的分类与回归模型。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

library(glmnet)
library(ISLR)
Hitters=na.omit(Hitters)
x=model.matrix(Salary~.,data=Hitters)[,-1]
y=Hitters$Salary
grid=10^seq(10,-2,length=100)
lasso.model=glmnet(x,y,alpha=1,lambda=grid)
#交叉验证，选择最优的lambda
cv.out=cv.glmnet(x,y,alpha=1,lambda=grid)
bestlam=cv.out$lambda.min
lasso.model2=glmnet(x,y,alpha=1,lambda=bestlam)
coef(lasso.model2)

20 x 1 sparse Matrix of class "dgCMatrix"
                     s0
(Intercept)  24.6396990
AtBat         .        
Hits          1.8499834
HmRun         .        
Runs          .        
RBI           .        
Walks         2.1959762
Years         .        
CAtBat        .        
CHits         .        
CHmRun        .        
CRuns         0.2058514
CRBI          0.4095910
CWalks        .        
LeagueN       .        
DivisionW   -99.9733911
PutOuts       0.2158910
Assists       .        
Errors        .        
NewLeagueN     .

通过这个实验可以看出，lasso的系数结果是稀疏的，19个预测变量中13个的系数为0。即使用交叉验证选择$\lambda$值建立的lasso模型仅包含6个预测变量。

(4) 基于树模型的特征选择在R中的实现：

在R语言中，基于树的模型，如随机森林、GBDT、XGBOOST等都可以输出变量的重要度，以随机森林为例。

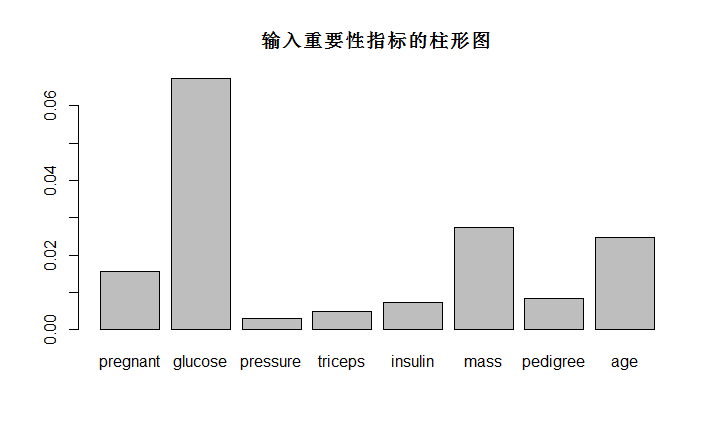
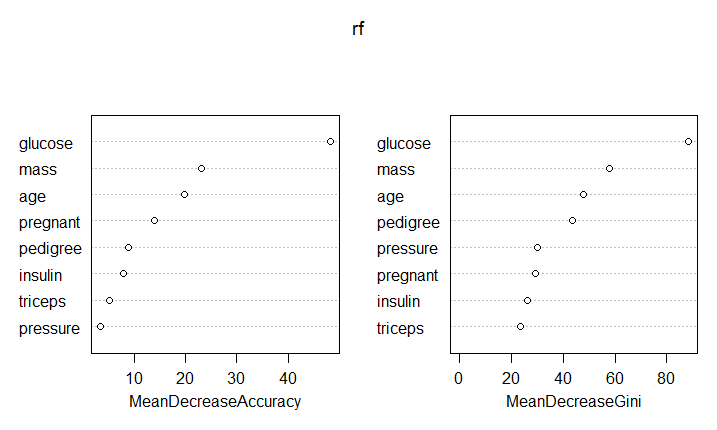
1
2
3
4
5
6
7
8
9
library(randomForest)
library(mlbench)  
# load the data  
data(PimaIndiansDiabetes) 
rf <- randomForest(x=PimaIndiansDiabetes[,1:8], 
          y=PimaIndiansDiabetes[,9],importance = T,ntree=500) 

barplot(rf$importance[,3],main="输入重要性指标的柱形图")
varImpPlot(rf,sort=TRUE,n.var=nrow(rf$importance))

输入重要性指标

平均精确率减少与平均不纯度减少

随机森林是基于决策树的集成模型，通过上图，我们可以很清楚地发现重要的特征。

###　(5)基于递归特征消除法的特征选择在R中的实现：

在R中，caret包可以使用递归特征消除法，主要使用rfe函数。

rfe参数说明：

x，预测变量的矩阵或数据框

y，输出结果向量（数值型或因子型）

sizes，用于测试的特定子集大小的整型向量

rfeControl，用于指定预测模型和方法的一系列选项

一些列函数可以用于rfeControl$functions，包括：线性回归（lmFuncs），随机森林（rfFuncs），朴素贝叶斯(nbFuncs)，bagged trees（treebagFuncs)和可以用于caret的train函数的函数（caretFuncs）。

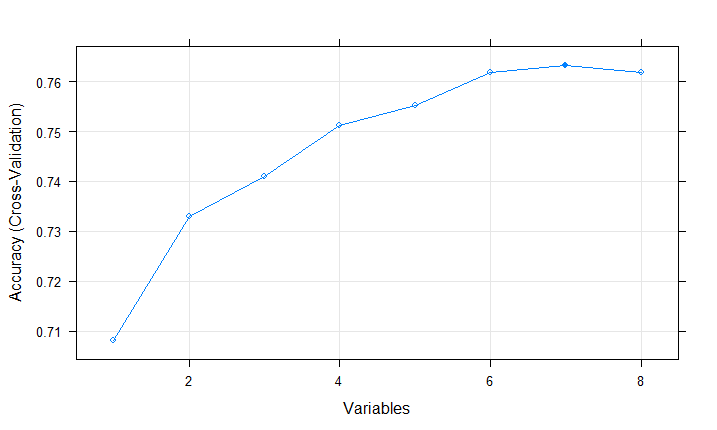
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#ensure the results are repeatable  
set.seed(7)  
#load the library  
library(mlbench)  
library(caret)  
# load the data  
data(PimaIndiansDiabetes)  
#define the control using a random forest selection function  
control <- rfeControl(functions=rfFuncs, method="cv", number=10)  
# run the RFE algorithm  
results <- rfe(PimaIndiansDiabetes[,1:8], 
               PimaIndiansDiabetes[,9], sizes=c(1:8), 
               rfeControl=control,metric = "Accuracy",ntree=100)  
#summarize the results  
print(results)  

Recursive feature selection
Outer resampling method: Cross-Validated (10 fold) 
Resampling performance over subset size:

 Variables Accuracy  Kappa AccuracySD KappaSD Selected
         1   0.7082 0.3030    0.04902  0.1181         
         2   0.7330 0.3920    0.06703  0.1564         
         3   0.7409 0.4115    0.06525  0.1582         
         4   0.7512 0.4409    0.06988  0.1691         
         5   0.7553 0.4452    0.07909  0.1911         
         6   0.7618 0.4583    0.08094  0.1897         
         7   0.7631 0.4620    0.08448  0.1927        *
         8   0.7617 0.4615    0.07810  0.1789         

The top 5 variables (out of 7):
   glucose, mass, age, pregnant, pedigree
#list the chosen features  
predictors(results)  

[1] "glucose"  "mass"     "age"      "pregnant" "pedigree" "insulin"  "triceps"

#plot the results  
plot(results, type=c("g", "o"))

image

从案例中可以看出，通过递归特征消除，发现用所有变量中的某7个自变量的模型是最好的，并且找出了最重要的5个特征。

4 结束语

特征工程是门艺术，也是每一个数据科学家的必修课，因此每个数据科学家既应该像一个统计学家和工程师，又应该像一个艺术家。

参考文献

[1] Dash M, Liu H. Feature selection for classification[J]. Intelligent data analysis, 1997, 1(3): 131-156.

[2]http://blog.datadive.net/selecting-good-features-part-i-univariate-selection/

[3]http://blog.datadive.net/selecting-good-features-part-ii-linear-models-and-regularization/

[4]http://blog.datadive.net/selecting-good-features-part-iii-random-forests/

[5]http://blog.datadive.net/selecting-good-features-part-iv-stability-selection-rfe-and-everything-side-by-side/

[6]http://scikit-learn.org/stable/modules/feature_selection.html#univariate-feature-selection

[7]http://blog.csdn.net/qtlyx/article/details/50780400

[8]http://minepy.readthedocs.io/en/latest/

[9]https://cran.r-project.org/web/packages/minerva/minerva.pdf

[10]http://machinelearningmastery.com/discover-feature-engineering-how-to-engineer-features-and-how-to-get-good-at-it/

[11]http://www.analyticsvidhya.com/blog/2016/03/select-important-variables-boruta-package/

[12]https://www.zhihu.com/question/28641663

[13]https://cran.r-project.org/web/packages/smbinning/smbinning.pdf

[14]http://www.scoringmodeling.com/rpackage/smbinning/

[15]蒋杭进. 最大信息系数及其在脑网络分析中的应用[D]. 中国科学院研究生院 (武汉物理与数学研究所), 2013.

机器学习特征选择

缺失值处理

数据缺失的概念

数据缺失是指在数据采集时由于某种原因应该得到而没有得到的数据。它指的是现有数据集中某个或某些属性的值是不完全的 。

数据缺失机制

在对缺失数据进行处理前，了解数据缺失的机制和形式是十分必要的。将数据集中不含缺失值的变量（属性）称为完全变量，数据集中含有缺失值的变量称为不完全变量。

  • 完全随机缺失（Missing Completely At Random,MCAR）：数据的缺失与不完全变量以及完全变量都是无关的。换句话说，某变量缺失值的出现完全是个随机事件。可以将存在MCAR变量的数据看做是假定完整数据的一个随机样本。
  • 随机缺失（Missing At Random,MAR）：数据的缺失不是完全随机的，数据的缺失只依赖于完全变量。例如，在一次测试中，如果IQ达不到最低要求的100分，那么将不能参加随后的人格测验。在人格测验上因为IQ低于100分而产生的缺失值为MAR。
  • 完全非随机缺失(Missing Not At Random,MNAR)：数据的缺失与完全变量自身有关，这种缺失是不可忽略的。例如，公司新录用了20名员工，由于6名员工表现较差在试用期内辞退，试用期结束后的表现评定中，辞退的6名员工的表现分即为非随机缺失。

从缺失值的所属属性上讲，如果所有的缺失值都是同一属性，那么这种缺失成为单值缺失，如果缺失值属于不同的属性，称为任意缺失。另外对于时间序列类的数据，可能存在随着时间的缺失，这种缺失称为单调缺失。

数据缺失的处理方法

缺失值处理的方法大致分为这几类：1、删除法；2、加权方法；3、基于插补的方法；4、基于模型的方法。

删除法

  • 删除观察样本

将存在缺失数据的样本删除，从而得到一个完备的数据集。这种方法简单易行，在对象有多个属性缺失值、被删除的含缺失值的对象与信息表中的数据量相比非常小的情况下是非常有效的。但是，在数据集中本来包含的样本很少的情况下，删除少量对象就足以严重影响数据的客观性和结果的正确性，因此，当缺失数据所占比例较大，特别当缺失数据是非随机分布时，这种方法可能导致数据发生偏离，从而导致错误的结果。

  • 删除变量

当某个变量缺失值较多，且对研究目标影响不大，可以将变量整体删除。

  • 改变权重

当删除缺失数据会改变数据结构时，通过对完整数据按照不同的权重进行加权，可以降低删除缺失数据带来的偏差。

删除法具有很大的局限性，它是以减少历史数据来换取信息的完备，会造成资源的大量浪费，丢弃了大量隐藏在这些对象中的信息。

加权方法

在进行抽样调查时，被调查者拒绝配合，会造成不响应调查现象。无不响应的抽样调查数据的随机化的推断，通常用它们的设计权加权抽取的单元。设计权是反比于它们的选取概率。设$y_{i}$是变量Y在总体中单元i的值，总体均值常用Horvitz-Thompson估计量进行估计
$$(\sum_{i=1}^{n} \pi_{i}^{-1} y_{i})(\sum_{i=1}^{n} \pi_{i}^{-1})^{-1}$$
其中$\pi_i$是单元i进入样本的已知概率，对不响应的加权方法是调整权以适应抽样设计时预料到的不响应。用
$$(\sum_{i=1}^{n}(\pi_{i} \hat{p}_{i})^{-1} y_{i} /\sum_{i=1}^{n}(\pi_{i} \hat{p}_i)^{-1}$$
替代Horvitz-Thompson估计量。${\hat{p}}_{i}$是单元i响应的概率的一个估计，通常它是样本的一个子类中的响应单元比例。

基于插补的方法

单一插补

单一插补指对每个缺失值，从其预测分布中取一个值填充缺失值后，使用标准的完全数据进行分析处理。

  • 均值插补

均值插补是在处理数据时可以把变量分为数值型和非数值型，如果是非数值型的缺失数据，运用统计学中众数的原理，用此变量在其他对象中取值频数最多的值来填充缺失值；如果是数值型的缺失值，则取此变量在其他所有对象的取值均值来补齐缺失值，这种方法只能在缺失值是完全随机缺失时为总体均值或总量提供无偏估计。但此方法使得插补值集中在均值点上，在分布上容易形成尖峰，导致方差被低估。可根据一定的辅助变量，将样本分成多个部分，然后在每一部分上分别使用均值插补，称为局部均值插补。

  • 利用哑变量进行调整

对缺失值创建一个指标，即设一个哑变量，1表示观测数据中存在缺失值，0表示观测数据中不存在缺失值，对缺失数据进行特定值的插补（如均值插补），这样做的好处是在缺失值处理时使用了全部变量的信息，但这样会导致估计有偏。

  • 热平台插补

对于一个包含空值的变量，本方法是在完整数据中找到一个与空值最相似的变量，然后用这个相似的值来进行填充。与均值插补法相比，热平台插补简单易懂还可以保持数据本身的类型，利用本方法填充数据后，其变量值与填充前很接近。它的主要缺点是不能覆盖已有数据没有反应的信息。

  • 冷平台插补

冷平台插补与热平台插补类似，但它是从过去的调查数据（如前期的调查数据或历史数据）中获得信息进行插补。冷平台插补同样不能消除估计的偏差。

  • k-means插补

利用辅助变量（即无缺失值的变量），定义样本间的距离函数，寻找与缺失值样本距离最近的无缺失值的n个样本，利用这n个样本的加权平均值来估计缺失数据。即利用聚类模型预测缺失变量的类型，再以该类型的均值进行插补，但这种方法在模型中引入了自相关，容易给后面的分析工作造成障碍。

  • 期望最大化（EM算法）

该算法的特点是通过数据扩张，将不完全数据的处理问题转化为对完全数据的处理问题，且通过假设隐变量的存在，简化似然方程，将比较复杂的似然函数极大似然估计问题转化为比较简单的极大似然估计问题。通过以下步骤实现：1、用估计值替代缺失值；2、参数估计；3、假定2中的参数估计值是正确的，再对缺失值进行估计；4、再估计缺失值。

随机插补

随机插补是在均值插补的基础上加上随机项，通过增加缺失值的随机性来改善缺失值分布过于集中的缺陷。

  • 贝叶斯Boostap方法

贝叶斯Boostap方法主要包括两步：1、从（0,1）均匀分布中随机抽取k-1个随机数，并进行排序记为$a_{1},a_{2},\cdots,a_{k-1}$，并且使得$a_{0}=0$且$a_{k}=1$，其中k是观测值的数目；2、对n个缺失值，分别从观测数据$x_{1},\cdots,x_{k}$中以概率$(a_{1}-a_{0}),(a_{2}-a_{1}),\cdots,(1-a_{k-1})$抽取一个值进行插补。

  • 近似贝叶斯Boostap方法

近似贝叶斯Boostap方法首先从k个观测数据集$x_{1},\cdots,x_{k}$中有放回的抽取$k^{}$个观测值建立一个新的数据集$x^{}$，对于n个缺失值，从数据集$x^{*}$中随机抽取n个值进行插补。

单一插补是标准的完全数据分析方法，要优于传统的忽略缺失值的思想，使得后续的统计分析可以在完整的数据集上进行，但单一插补的插补数据都是唯一的,插补结果扭曲了样本中变量的分布，容易低估估计量的方差。

多重插补

与单一插补方法相比较，多重插补方法充分地考虑了数据的不确定性。多重插补的主要分为三个步骤，综合起来即为：插补、分析、合并。插补步是为每个缺失值都构造出 m 个可能的插补值，缺失模型具有不确定性，这些插补值能体现出模型的这个性质，利用这些可能插补值对缺失值进行插补就得到了 m 个完整数据集。分析步是对插补后的 m 个完整数据集使用一样的统计数据分析方法进行分析，同时得到 m 个统计结果。综合步就是把得到的这 m 个统计结果综合起来得到的分析结果，把这个分析结果作为缺失值的替代值。多重插补构造多个插补值主要是通过模拟的方式对估计量的分布进行推测，然后采用不同的模型对缺失值进行插补，这种插补是随机抽取的方式，这样以来能提高估计的有效性和可靠性。

多重插补法主要有以下几种：

  • PMM法(Predictive Mean Matching,PMM)

PMM法也称随机回归插补法,它是回归插补法的变形,插补值是由回归模型的的预测值加上一个随机产生的误差项结合而成.一般而言,对应于某种确定性的插补方法,可以产生出相应的随机性插补方法.它的优点是能够在正态性假设不成立的情况下插补适当的值,缺点是随机误差项的确定比较困难.

  • 趋势得分法(Propensity Score, PS)

趋势得分是在给定观测协变量时分配给一个特殊处理的条件概率，它对每个有缺失值的变量产生一个趋势得分来表示观测缺失的概率。之后,根据这些趋势得分,把观测分组,最后再对每一组数据应用近似贝叶斯Bootstrap插补。

  • 马尔科夫链蒙特卡罗法(Markov Chain Monte Carlo,MCMC)

MCMC方法是蒙特卡洛重要抽样, 是流行的贝叶斯分析方法中计算后验期望的方法。一般地,MCMC将缺失数据视为参数,然后将这些参数纳入抽样的范围即可。MCMC方法对缺失数据的处理相对灵活、简单易行。

多重插补方法有着其他插补方法所不具备的独特优势，第一，与其他方法相比较，多重插补方法能够尽可能的利用其他辅助信息，给出多个替代值，保持了估计结果的不确定性的大量信息；第二，多重插补方法能够尽可能接近真实情况下去模拟缺失数据的分布，在这样的条件下能够尽可能的保持变量之间的原始关系；第三，在多重插补的插补步骤会产生多个插补值，这样以来就可以利用这些不同的替代值来进一步反映无回答的不确定性。

几何插补

几何插补就是从几何的观点来研究插补，在可忽略的缺失机制下，假定观测数据的主成分与完全数据的主成分相同，那么可以通过寻找观测数据的主成分进行插补，换句话说就是用逼近观测数据的方法去插补缺失数据。

基于模型的方法

这类方法适用于大多数场合。一般对观测数据定义一个模型，然后在模型下根据适当的分布做推断。这个方法的优势就是灵活：回避特殊情况的方法，在模型假定基础上产生的方法可以进行推演和评价；以及考虑数据不完整性时方差分析的可用性。

基于模型的方法既不是删除缺失值也不是采用插补方法去补全缺失值，而是首先要考虑缺失数据的缺失机制，在此基础上为部分缺失数据定义模型，模型的参数可以通过极大似然或极大后验估计，以完全信息极大似然估计为例，这是基于模型的方法，可直接用于不完全数据的分析的，最大的特点在于即使缺失数据不是完全随机缺失，估计的结果也是无偏的。完全信息极大似然估计是建立在对数极大似然估计基础上的，假定数据来源于多元正态分布，对于不完全服从多元正态的数据还是稳健的极大似然估计的不足之处在于需要相对比较大的数据集，而且可供推断的信息是有限的。当样本量太小时，不宜采用完全信息极大似然估计。

不对缺失值进行处理

直接在包含空值的数据上进行数据挖掘。可通过贝叶斯网络和人工神经网络实现。

贝叶斯网络是用来表示变量间连接概率的图形模式，它提供了一种自然的表示因果信息的方法，用来发现数据间的潜在关系。在这个网络中，用节点表示变量，有向边表示变量间的依赖关系。贝叶斯网络仅适合于对领域知识具有一定了解的情况，至少对变量间的依赖关系较清楚的情况。否则直接从数据中学习贝叶斯网的结构不但复杂性较高（随着变量的增加，指数级增加），网络维护代价昂贵，而且它的估计参数较多，为系统带来了高方差，影响了它的预测精度。当在任何一个对象中的缺失值数量很大时，存在指数爆炸的危险。

基于神经网络进行缺失数据估计的基本思想是：把同一系统的除待估计参数以外的其它参数的数据作为网络的输入，待估计参数的数据作为输出，利用该系统中的已知数据训练网络，在网络满足要求后，把与待估计的数据同一时间的其它参数的数据输入网络，网络输出值即为缺失数据的估计值。

机器学习数据预处理

逻辑回归的前世今生

引子

大家在日常的工作和学习中是不是经常有这样的疑问：邮箱是如何自动区分正常邮件和垃圾邮件的呢？银行是如何判断是否通过你的贷款申请的呢？经常收到某种商品的推荐信息，商家又是如何知道你对这个商品感兴趣的呢？

为了回答上述疑问，这一期给大家介绍逻辑回归算法。逻辑回归，也称Logistic Regression,主要区别于一般的线性回归模型。我们知道，一般的线性回归模型都是处理因变量是连续变量的问题，如果因变量是分类变量，一般线性回归模型就不再适用。逻辑回归算法因其原理的相对简单，可解释性强等优点已成为互联网领域最常用也最有影响力的分类算法之一，同时它还可以作为众多集成算法以及深度学习的基本组成单位，所以学好逻辑回归尤其重要。

我们知道，一般的线性回归模型都是处理因变量是连续变量的问题，如果因变量是定性变量，一般线性回归模型就不再适用了。

或许有人会有疑问，为什么对于分类问题，逻辑回归行而一般的线性回归模型却不行呢？二者的区别又是什么呢？下面将从现实意义和数学理论上给出解释。

定性因变量回归方程的意义

设因变量y是只取0,1两个值，考虑简单线性回归模 $y=\beta_{0}+\beta_{1}x_{i} +\varepsilon$
在这种y只取0和1两个值的情况下，因变量均值 $E(y_{i})=\beta_{0}+\beta_{1}x_{i}$ 有着特殊的意义。
由于$y$是0-1型随机变量，得到如下概率分布
$$ P(y = 1)= p$$
$$ P(y = 0)= 1-p $$
根据离散型随机变量期望值的定义，可得
$$ E(y)=1( p )+0(1-p)= p $$
所以，作为由回归函数给定的因变量均值，$E(y)=\beta_{0}+\beta_{1}x$是自变量水平为$x$时$y=1$的概率。

逻辑回归模型的特别之处

对于一般的线性模型
$$y=\beta_{0}+\beta_{1}x +\varepsilon$$
误差项有大三假定条件：

（1）误差项$\varepsilon$是一个期望为0的随机变量，即$E(\varepsilon)=0$

（2）对于所有的$x$，$\varepsilon$的方差都相同，这意味着对于一个特定的x值，y的方差也都等于$\sigma^2$。

（3）误差项$\varepsilon$是一个服从正态分布的随机变量，且相互独立，即$\varepsilon\sim N(0,\sigma^2)$。

而在因变量y只能取0和1的逻辑回归模型，误差项 $\varepsilon=y-(\beta_{0}+\beta_{1}x)$ 显然是两点型的离散分布，不满足误差项正态分布的基本假定；同时误差项的方差 $Var(\varepsilon_{i})=Var(y_{i})=(\beta_{0}+\beta_{1}x_{i})(1-\beta_{0}-\beta_{1}x_{i})$,可以看出误差项随着$x$的不同水平而变化，是异方差，不满足线性回归的基本假定；当因变量为0和1时，回归方程代表的是概率分布，所以因变量的均值受到如下限制$0\leq E(y_{i})\leq1$,一般的线性回归方程不会有这种限制。而逻辑回归却利用一些数学变化巧妙的解决了这些的问题，请看下面一节。

从一般线性回归到逻辑回归

当被解释变量$y$为0和1的二分类变量时，虽然无法采用一般的线性回归模型建模，但是可以借鉴其理论基础：

第一，一般线性模型$p(y=1|x)=\beta_{0}+\beta_{1}x_{1}+\dots+\beta_{p}x_{p}$，方程左侧的概率$p$的取值范围为[0,1]，方程右边的额取值范围在$-\infty\sim +\infty$之间。如果对概率p做合理的变换，使其的取值范围与右侧吻合，则左侧和右侧可以通过等号连接起来。

第二，一般线性模型$p(y=1|x)=\beta_{0}+\beta_{1}x_{1}+\dots+\beta_{p}x_{p}$，方程中的概率$p$与解释变量之间的关系是线性的。但在实际的应用中，它们之间的关系往往是非线性的。例如通过银行贷款申请的概率通常不会随着年收入（或者年龄等）的增长而线性增长。于是对概率$p$的变换应该是采用非线性变换。

基于以上的分析，可采取一下两步变换：

第一步，将概率$p$转换成$\Omega:\Omega=\frac{p}{1-p}$。其中，$\Omega$称为优势，是事件发生的概率与不发生的概率之比。这种变换是非线性的，且$\Omega$是$p$的单调函数，保证了$\Omega$和$p$增长的一致性，是模型易于理解。优势的取值范围在0和无穷大之间。

第二步，将$\Omega$换成$ln\Omega:ln\Omega=ln\frac{p}{1-p}$。其中，$ln\Omega$称为$logit P$.

上述的两步变换称为logit变换。经过logit变换，$logit P$的取值范围范围$-\infty\sim+\infty$，与一般线性回归模型右侧的取值范围吻合。同时$logitP$与$p$之间保持单调一致性。

至此，用等号将$logitP$和一般线性模型的右侧连接起来，得到$logit P=\beta_{0}+\beta_{1}x_{1}+\dots+\beta_{p}x_{p}$,即为逻辑回归模型。这样我们就完成从一般线性模型到逻辑回归模型的演变。

或许有人还会质疑logit变换的合理性，那么我们就继续往下扒。
从以上的推导和变换我们得到，$$ln\frac{p}{1-p}=\beta_{0}+\beta_1 x_{1}+\beta_2 x_{i}+\cdots +\beta_p x_{p}$$
故有 $p=\frac{1}{1+e^{-(\beta_{0}+\beta_1 x_{1}+\beta_2 x_{2}+\cdots +\beta_p x_{p})}}$，其为(0,1)型的Sigmoid函数，如下图所示。这是一个非线性函数，很好的体现了概率$p$与解释变量之间的非线性关系。

逻辑回归模型的解读

逻辑回归方程的右侧与一般线性回归方程的形式一致，可用类似的方法解释逻辑回归方程系数的含义，即当其他自变量保持不变时，自变量$x_i$每增加一个单位，$logitP$平均增加（或减少）$\beta_{i}$个单位。

在实际应用中，人们更关心自变量为优势$\Omega$带来的变化，其中优势$\Omega=\frac{p}{1-p}$，表示某一事件的发生概率与不发生概率之比。同时我们还会通过优势比来进行不同组别之间风险的对比分析。

在逻辑回归方程中，$\Omega=e^{(\beta_{0}+\beta_1 x_{1}+\beta_2 x_{2}+\cdots +\beta_p x_{p})}$，当其他自变量不变时，$x_{i}$每增加一个单位，优势变为原来优势的$e^{\beta_i}$倍，优势比即为$e^{\beta_i}$。

逻辑回归模型的参数估计

设y是0-1型变量，$x_{1},x_{2},\cdots ,x_{p}$是与y相关的确定性变量，n组观测数据为$(x_{i1},x_{i2},\cdots ,x_{ip};y_{i})(i=1,2,\cdots,n)$,其中，$y_{1},y_{2},\cdots ,y_{n}$是取值0或1的随机变量，$y_{i}$与$x_{i1},x_{i2},\cdots ,x_{ip}$的关系如下：
$$E(y_{i})=p_{i}=f(\beta_{0}+\beta_1 x_{i1}+\beta_2 x_{i2}+\cdots +\beta_p x_{ip})$$
其中，函数f(x)是值域在[0,1]区间内的单调增函数。对于逻辑回归
$$f(x)=\frac{e^{x}}{1+e^{x}}$$
于是$y_{i}$是均值为$p_{i}=f(\beta_{0}+\beta_1 x_{i1}+\beta_2 x_{i2}+\cdots +\beta_p x_{ip})$的0-1分布，概率函数为
$$P(y_{i}=1)=p_{i}$$ $$P(y_{i}=0)=1-p_{i}$$
可以把$y_{i}$的概率函数合写为
$$P(y_{i})=p_{i}^{y_{i}}(1-p_{i})^{1-y_{i}},y_{i}=0,1;i=1,2,\cdots,n$$
于是，$y_{1},y_{2},\cdots ,y_{n}$的似然函数为
$$L=\prod_{i=1}^{n}P(y_{i})=\prod_{i=1}^{n}p_{i}^{y_{i}}(1-p_i)^{1-y_i}$$
对似然函数取自然对数，得
$$lnL=\sum_{i=1}^{n}[y_i lnp_i+(1-y_i)ln(1-p_i)]\\ =\sum_{i=1}^{n}[y_i ln\frac{p_i}{(1-p_i)}+ln(1-p_i)]$$
对于logistic回归，将
$$p_i=\frac{e^{(\beta_{0}+\beta_1 x_{i1}+\beta_2 x_{i2}+\cdots +\beta_p x_{ip})}}{1+e^{(\beta_{0}+\beta_1 x_{i1}+\beta_2 x_{i2}+\cdots +\beta_p x_{ip})}}$$
代入得
$$lnL=\sum_{i=1}^{n}[y_i (\beta {0}+\beta_1 x_{i1}+\beta_2 x_{i2}+\cdots +\beta_p x_{ip})-ln(1+e^{(\beta_{0}+\beta_1 x_{i1}+\beta_2 x_{i2}+\cdots +\beta_p x_{ip})})]$$
最大似然估计就是选取$\beta_{0},\beta_1,\beta_2,\cdots ,\beta_p$的估计值$\hat{\beta}_0,\hat{\beta}_1,\hat{\beta}_2,\cdots,\hat{\beta}_p$，使上式最大。同时，作为一个最优化问题，可以采用梯度下降法和牛顿法等最优化算法。

逻辑回归模型的检验

逻辑回归方程的显著性检验的目的是检验所有自变量与$logitP$的线性关系是否显著，是否可以选择线性模型。原假设是假设各回归系数同时为0，自变量全体与$logitP$的线性关系不显著。如果方程中的诸多自变量对$logitP$的线性解释有显著意义，那么必然会使回归方程对样本的拟合得到显著提高。可通过对数似然比测度拟合程度是否有所提高。

我们通常采用似然比检验统计量$-ln(\frac{L}{L_{x_{i}}})^2$也可称为似然比卡方,其中$L$表示引入变量$x_{i}$前回归方程的似然函数值，$L_{x_{i}}$表示引入变量$x_{i}$后回归方程的似然函数值。似然比检验统计量越大表明引入变量$x_{i}$越有意义。如果似然比卡方观测值的概率p值小于给定的显著性水平，不接受原假设，即认为自变量全体与$logitP$之间的线性关系显著。反之，线性关系不显著。

回归系数的显著性检验

逻辑回归系数的显著性检验是检验方程中各变量与$logitP$之间是否具有线性关系。原假设是假设变量$x_{i}$与$logitP$之间的线性关系不显著，即$\beta_{i}=0$。

后记

逻辑回归虽然虽然简单，但是因为其运算过程简单，而且分类效果不会太差，所以在业界应用广泛。我们大名鼎鼎的围棋高手AlphaGo在快速走子的过程中，也有用到该算法哟。

机器学习逻辑回归
,